Some photography for art's sake

Palm fronds, April 11, 2023. Copyright 2023 Melody M. Covington.

Sunset clouds, April 16, 2023. Copyright 2023 Michael A. Covington.

Permanent link to this entry

Why specialty retail chains are shrinking

CNN has a nice opinion piece about why Radio Shack, Toys 'R' Us, and Bed Bath and Beyond failed, and Staples and Barnes & Noble have shrunk.

Stripped of jargon, their point is that the selling point of each of these was to offer a very complete selection of one category of products. And that is something on which online shopping will always win — always offering an even more complete selection. Local shopping is dropping back to providing only the more commonly needed items, as was normal before the specialty-shopping buildup of the mid-1990s.

The article also say something about a decrease in the amount of "stuff" people want to "accumulate." I think they missed a big point there. Due to microelectronics and some other technical advances, a lot of "stuff" underwent major improvements in performance or versatility in the 1990s and early 2000s. (Compare an ordinary person's camera in 1990 and 2010.) Those changes have slowed down. There aren't as many new things to want, and what you bought 10 years ago is probably still satisfactory.

Permanent link to this entry

Museum Day

April 28 is the anniversary of Melody's and my first date, a trip to the Georgia Museum of Art, and we re-enacted the trip two years ago (at the museum's new location). Yesterday we decided to visit the museum again, and in fact to do so every April 28 from here on.

We saw an exhibit of important and interesting art lent by Princeton University, marred only by a set of explanatory placards that unfortunately were focused on contemporary political correctness rather than the works of art. But there was one humorous item: a 1880s Native American sculpture from New Mexico, of a white figure with two heads (with big mouths) and four arms, obviously a caricature of the typical fast-talking hand-waving gringo tourist, made, as we understand it, to be sold to a gringo tourist.

Permanent link to this entry

What is a chatbot?

Just a moment to clear up the meaning of a word we're suddenly hearing everywhere: chatbot.

A chatbot ("chatting robot"), or chat program, is a computer program that carries on a conversation with you in plain English, usually in a very limited way. They've existed since the 1960s. We used to demonstrate BASIC by writing programs that would carry on conversations like this:

WHAT IS YOUR NAME? Michael
GOOD TO MEET YOU, MICHAEL.
ARE YOU HAVING A GOOD DAY? yes
I'M GLAD TO HEAR THAT.

and so on. At the time, this was just a novelty, a humorous demonstration that computer programs could interact with users. But chatbots have been used a lot in the business world to field questions expressed in plain English and attempt to deliver answers.

Naturally, for that to work, the answers have to be controlled. If you ask the bank's chatbot what your balance is, you want it to actually look at the bank's records and retrieve the true answer, not make up something at random.

And that is the problem. Generative chatbots such as ChatGPT make up answers at random, based only on knowledge of how words are used. This is not something that will change as their training sets become bigger and better. It can only be changed by constructing them in a deeply different way.

Generative technology could be quite useful on the input side, recognizing different ways of phrasing the same question. But the information given out by computers needs to remain controlled and reliable. Mis-recognition is less of a risk, if you can be sure that even if the computer is answering the wrong question, it's giving out true information.

Permanent link to this entry

It's galaxy season!

Amateur astronomers call this time of year "galaxy season" because the earth's position in its orbit puts us in a good position for seeing distant galaxies — we're facing away from the plane of our own galaxy. That will change when the summer Milky Way comes into view. But right now, we can see a lot of galaxies, and what's more, we're having an unprecedented spell of clear weather; I've done astrophoto sessions (in my driveway) on 4 of the past 5 nights.

I'm taking the opportunity to familiarize myself with one particular setup, using it over and over to get used to what's new. I'm taking pictures that resemble pictures I have taken before with slightly different equipment; I call this "teaching a new dog old tricks" and the goal is to give the equipment (including software) a good shakedown and build my familiarity with it.

The setup consists of an AT65EDQ 6.5-cm f/6.5 apochromatic refractor, Canon 60Da camera (at ISO 640), Losmandy GM811G mount, iOptron iGuider mini-guidescope and camera mounted on the side of the Losmandy mount's saddle, and a Thinkpad T490s with N.I.N.A. and PHD2 software controlling everything. For years I've been complaining that we get new software versions more often than we get clear nights. Not this week!

To start, I re-did the picture of the M95 region from the previous week, with the focus adjusted a bit better:

The most prominent galaxies, from top to bottom, are NGC 3384, M105, NGC 3389, M96, and M95. This is a stack of 20 2-minute exposures, just like the previous one. But I think it looks a bit better.

M51

That same evening (April 18), I took aim at M51, one of the first galaxies to be recognized as spiral:

Under ideal conditions, this spiral structure can be seen in a telescope, but I have never seen it; most of the structure of galaxies shows up only on photographs. This is a stack of 29 2-minute exposures. I can see at least four other galaxies in the background.

Permanent link to this entry

M81 and M82

Here are M81 and M82 in Ursa Major, which I've photographed many times, along with NGC 3077 at the lower left. Stack of 33 2-minute exposures.

Permanent link to this entry

M65, M66, and a hamburger

Here are M65 and M66 in Leo, and, at the top, NGC 3628, often called the Hamburger Galaxy because of its unusual edge-on appearance. The three are called the Leo Triplet (the word triplet can mean either a group of three, or a person who was born with two siblings, and here it means the former).

Permanent link to this entry

Something closer to home

Finally, here's the nearby star cluster M44 in the constellation Cancer. I was having trouble with my mount — as it turned out, it was out of balance — and by the time I got it working well, there was only time for four 2-minute exposures before the star cluster set behind the trees.

They aren't visible here, but there are at least half a dozen distant galaxies potentially visible between the stars in this cluster. (Some of them were barely visible when I was processing the image.) I want to go back and get a picture of M44 that will show them clearly.

Permanent link to this entry

PEMDAS is not the whole truth
Implicit multiplications are done first

Before someone gets you into an argument on the Internet about a formula such as

8÷2(4−2)

hear me out. People will tell you that because of the PEMDAS rule, you have to deal with Parentheses, then Exponents (none here), then Multiplication and Division in one pass left to right, then Addition and Subtraction in one pass left to right. So you're supposed to calculate:

8÷2(4−2)
8÷2×2
4×2
8

I call foul, and so does my Sharp calculator:

Contrast with:

What's going on? The multiplication by 2 in the formula we were given is an implicit multiplication, notated by just writing things next to each other without an ×.

In many mathematics books, and on many calculators, implicit multiplications are done before other multiplications and divisions. So I calculate:

8÷2(4−2)
8÷2(2)
8÷4
2

Look at some algebra books for yourself. If you see 1/2x it almost certainly means 1/(2x). The same goes for 1/2π, and my calculator agrees:

In any case, this isn't a controversy about mathematics. It is about the grammar and style, so to speak, of formulae. Different mathematicians throughout history have written formulae a bit differently from each other — look at a British math book from a century ago, for example — and the intelligent reader will try to understand what the author actually means, rather than bashing someone over the head with PEMDAS.

I thank Steve Tonkin for pointing out to me that calculators recognize this.

[Note added May 14:] My good friend Doug Downing points out a problem with the formula 8÷2(4−2).

The symbol ÷ is simply not used in adult-level mathematics books. In college mathematics, science, and engineering, fraction bars are used wherever possible, and they automatically show grouping. Occasionally, simple formulae use / for division, but only when the context is clear.

I'll add that × is also uncommon, although I've used it in formulae where some of the items being multiplied are expressed as words, or consecutive items are numbers.

More generally, as I've noted before, alternating multiplications and divisions simply aren't written. They are signs of a disorganized formula. As far as possible, items that are to be multiplied are grouped together, and divisions are brought out by fraction bars, or at least by expressions like ab/cd (which is understood as (ab)/(cd) because implicit multiplications group more tightly than multiplication signs).

Finally, a good mathematics writer doesn't throw PEMDAS challenges at you. Parentheses aren't expensive. Use them!

Permanent link to this entry

Galaxies in Leo: M95, M96, M105

We get new versions of important astronomy software more often than we get clear nights. So last night's project was very much "teaching a new dog old tricks" — doing things I've already done, but trying out a new combination of equipment and software.

This is a stack of 20 2-minute exposures with an AT65EDQ refractor (6.5-cm f/6.5) and Canon 60Da. The most prominent galaxies, from top to bottom, are NGC 3384, M105, NGC 3389, M96, and M95. This is only part of the picture, cropped.

I've mounted an iOptron iGuider on the side of my Losmandy mount saddle. It gives 6.44 arc-seconds per pixel, which seems too big to do any good, but actually, it can guide to about 1.5 arc-seconds most of the time, and that's good enough with this setup, which gives about 2 arc-seconds per pixel. Here you see it on the left, without its cable attached:

The camera is the old Canon 60Da (vintage 2012); I'm still confirming that, knowing what I now know about exposures, I can get it to perform as well as the newer Nikon D5500, but without the Nikon's quirks.

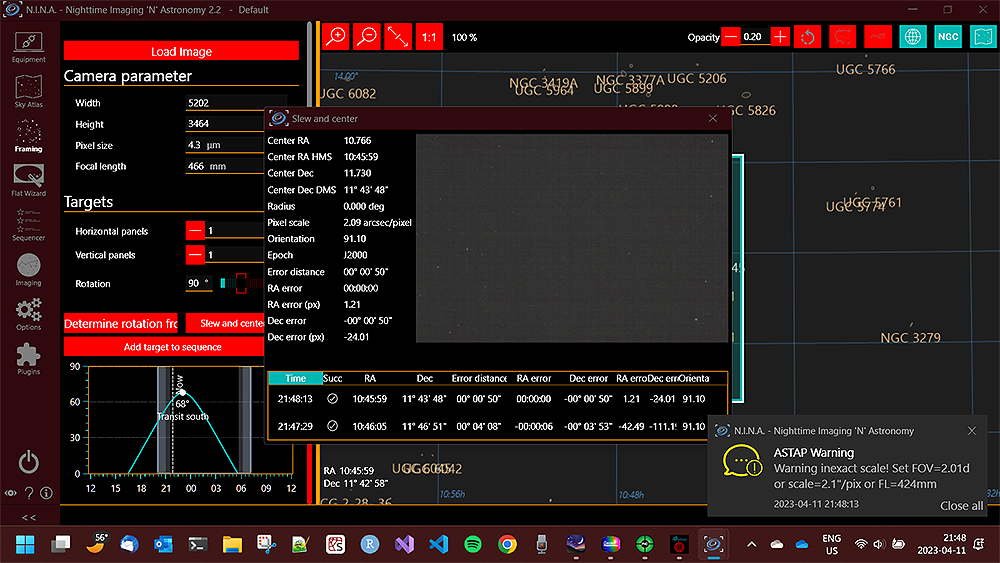
But the most complicated part of the new setup is that I am now controlling everything with N.I.N.A. software, which is powerful but moderately complicated. It's designed for fully automated observatories, although I don't use its full capabilities. In this screenshot you see it after it has just aimed the telescope and plate-solved (i.e., has taken a short exposure and compared to a built-in star atlas), and then nudged the telescope a short distance, to get the specified object right in the center. And it figured out I had given it the wrong focal length for the telescope, and handily gave me the correct number.

Permanent link to this entry

True focal length of the Celestron 8 EdgeHD

I've had my Celestron 8 EdgeHD telescope since 2014 and have been mistaken about its focal length the whole time. But it's not my fault.

I know the focal length of a Schmidt-Cassegrain varies with the position of the focal plane, and that's the traditional reason for not being very precise about it. But this is no ordinary Schmidt-Cassegrain. This is an EdgeHD, whose focal plane needs to be — and is — held in a particular position for best field flatness. I use Celestron's own camera adapters to put the camera sensor exactly there.

The ring on the front of the telescope says "FL 2000 MM F/10." The specifications and instruction manual say the diameter is 203.2 mm, the focal length is 2032 mm, and it's f/10.

But the famous EdgeHD White Paper says 203.2, 2125 (!), and f/10.4. That's different enough not to be within the margin of error. What should I believe?

I asked the question on Cloudy Nights and was quickly reminded that the focal length can be measured by plate-solving pictures on Astrometry.NET to find out their exact scale, if you know the sensor dimensions of your camera. A couple of people posted measurements of their own, and I also made mine, using existing pictures from eight years ago or so, taken with the Canon 60Da.

Bearing in mind that due to limited decimal places, I only know the sensor dimensions to within slightly better than 1%, I got a focal length of 2112 mm without the ×0.7 compressor and 1483 mm with it. A further test with a Nikon D5500 image, with the compressor on, gave 1481 mm. These are within the margin of error of the figures given in the white paper, 2125 and (implicitly) 1488, so I think the latter are correct. (See further tests on May 6.) There could also be some variation between individual telescopes or manufacturing runs, depending on how the final figuring of the optics is done.

How did I get into all this? Trying to figure out whether the full face of the moon will fit on a Canon APS-C sensor when the ×0.7 compressor is in place. The answer? Yes, but sometimes it's a very tight fit, if the moon is full and near perigee. More often it's easy, because the moon is not at perigee, or is not full (so we can cut off part of the unlit side), or both.

This should give very sharp moon images, and I'm going to pursue it.

Permanent link to this entry

Another ETX moon

I got the ETX out on the Losmandy mount again last night (April 2) and photographed the moon again, with the same setup as the previous day, but in steadier air. This picture convinces me that the ETX-90 is optically completely up to this task. Field curvature does not seem to be a problem.

Permanent link to this entry

ETX moon

I've temporarily taken the ETX-90EC off its computerized fork mount and attached a dovetail so I can put in on my equatorial mounts (and have room for camera adapter!). Yesterday evening, before dark, I attached the shorter version of the camera adapter (T-adapter) and my Canon 60Da and got this picture of the moon in the blue sky, in somewhat unsteady air.

What I confirmed is that the full face of the moon will fit on an APS-C camera sensor — just barely. (It can be 14% larger than shown in this picture.) You can see how the light falls off at the corners of the picture, although the contrast enhancement that I performed exaggerates it. There is just enough room in the middle for a centered image of the moon, untouched by vignetting.

I know there would be less vignetting if I used the longer version of the camera adapter, but then the image would be larger, and the moon would not fit into the frame. In fact, the focal length would be longer than with my C8 and compressor, and I'd use that instead.

So I have a telescope that can go on the equatorial mounts and take full-face pictures of the moon or sun. Whether that's going to be the long-term best use of the ETX-90, or whether I should sell it, or put it back on its computerized mount and use it that way, I am not yet sure.

Looking at Gamma Leonis with a 5-mm eyepiece (250×, which is extremely high power for such a small telescope), I saw good star images in focus, although outside of focus, the telescope seemed to be slightly out of collimation. This, I'm told, is a well-known quirk of the ETX-90.

Permanent link to this entry

A bit of science humor for April 1

Approximations to π used in various fields:

Mathematics: 3.14159265

Engineering: 3.14

Astrophysics: 1, or maybe 10

Computer science: O(1)

Permanent link to this entry